leetcode 最长回文子串问题

今天刷leetcode时遇到的最长回文子串问题：

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
输入: "cbbd"
输出: "bb"

我用的是Manacher算法算法，时间复杂度O(n)），为什么代码在执行时反倒没有中心扩展算法（时间复杂度O(n^2)）的快呢？

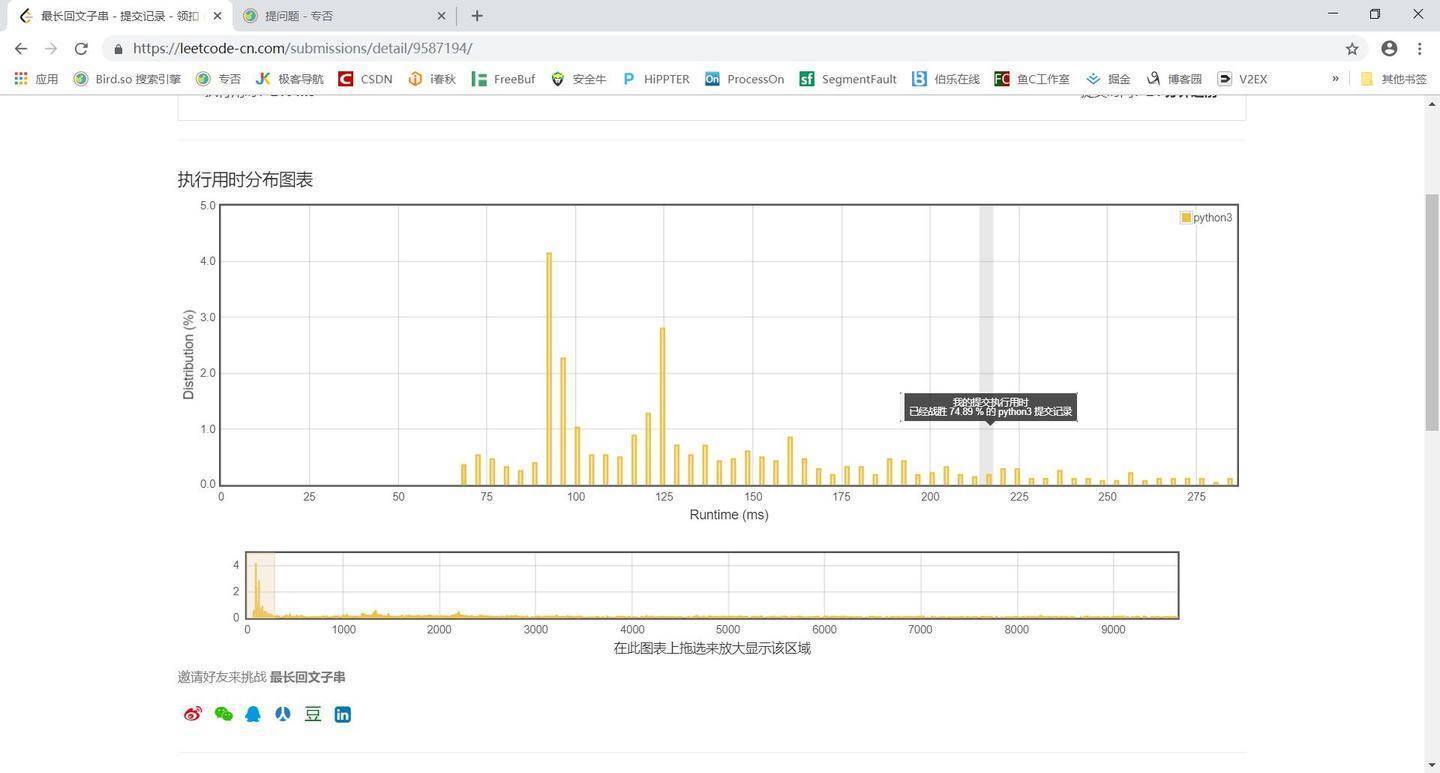
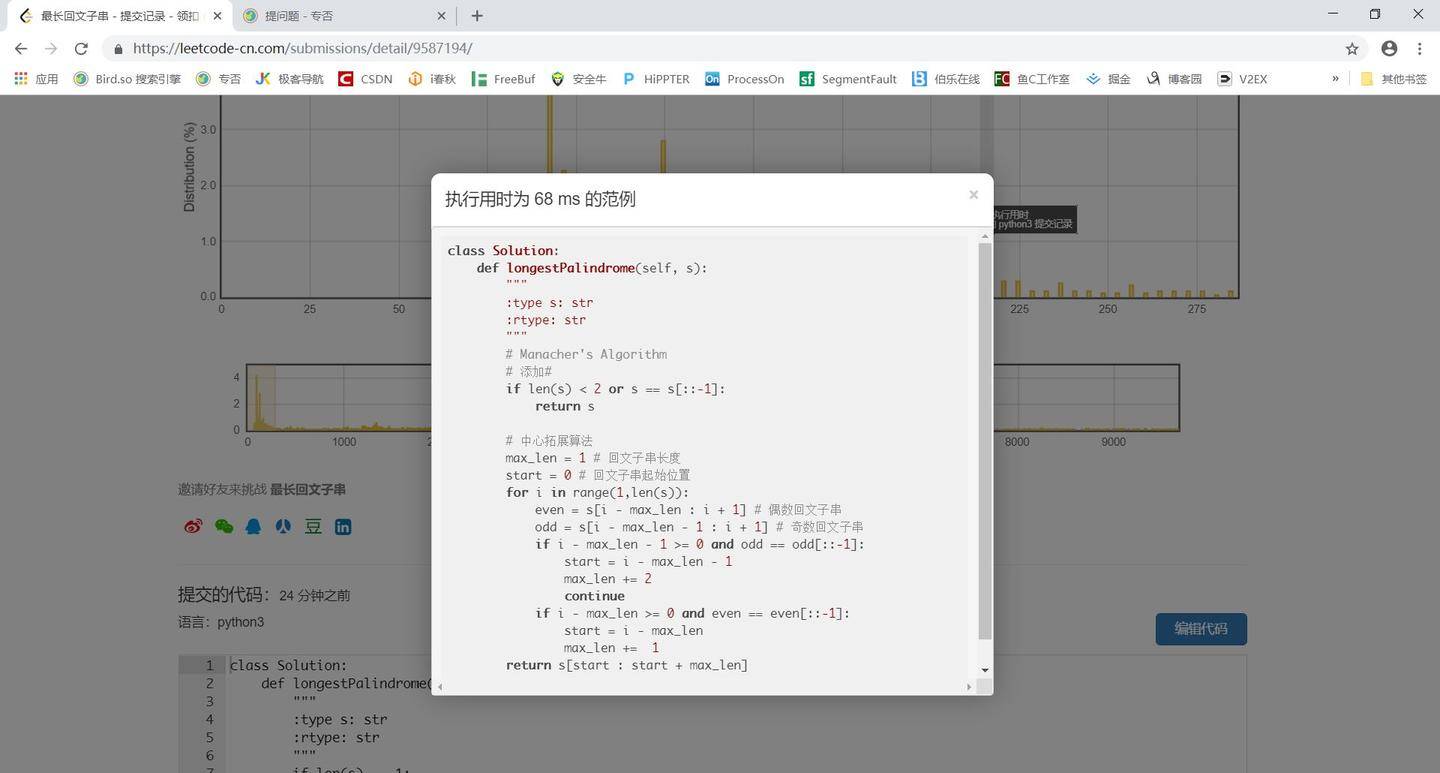
下面是我的代码：

class Solution:
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if len(s) == 1:
            return s
        # 预处理，添加字符'#'解决字符串长度分奇偶的问题
        ss = '#' + '#'.join(s) + '#'
        
        # 初始化
        pos = 0                           # 对称轴
        maxpos = 0                        # 最大位置
        maxright = 0                      # 最大右边界
        lenss = len(ss)                   # 字符串长度
        p = [0] * lenss                   # 对称半径列表
        
        # 主循环
        for i in range(lenss): 
            # 判断是否在右边界以内
            if i < maxright:
                # 设置p[i]的值
                p[i] = min(p[2*pos-i], maxright-i)
            else:
                p[i] = 1
            
            # 当没有到字符串首或尾时扩展边界
            while ((i - p[i]) > 0) and ((i + p[i]) < lenss) and (ss[i-p[i]] == ss[i+p[i]]):
                p[i] += 1
            
            # 更新边界
            if maxright < i + p[i] -1:
                maxright = i + p[i] -1
                pos = i
            
            # 更新最大索引
            if p[i] > p[maxpos]:
                maxpos = i
        
        return ss[maxpos-(p[maxpos]-1):maxpos+p[maxpos]].replace('#','')